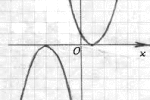
Условие задачи. Квадратный трехчлен f(х) имеет ровно один корень. Кроме того, уравнение f(2х — 3) + f(3х + 1) = 0 имеет ровно один корень. Найти корень трехчлена (приведите все … читать далее
|
|||||
Основатель школы Федор Борисович Смирнов
e-mail: repetitorFB@gmail.com |
Эту задачу решали ученики 7-9 классов на школьном этапе Всероссийской олимпиады 2013-2014 г. по математике в Москве. Условие задачи Назовем число зеркальным, если слева направо оно «читается» так же, как … читать далее Эта задача предлагалась ученикам 8-9 классов на школьном этапе Всероссийской олимпиады 2013-2014 г. по математике в Москве. Условие задачи Каково отношение площади закрашенной части к белой (вершины всех квадратов за … читать далее Эту задачу предлагали решить ученикам 9-11 классов на школьном этапе Всероссийской олимпиады 2013-2014 г. по математике в Москве. Условие задачи Вася задумал два числа. Их сумма равна их произведению и … читать далее 1. Замените в выражении (х3 — 2)2 + (х2 + *)2 звездочку (*) на одночлен так, чтобы после возведения в квадрат и приведения подобных слагаемых получилось четыре слагаемых. 2. Каково … читать далее На школьном этапе Всероссийской олимпиады 2013-2014 г. по математике в Москве задачу про гномов предлагали решить ученикам 8-11 классов. Условие задачи. Каждый из 10 гномов либо всегда говорит правду, либо … читать далее
|
|
|||
|
Powered by WordPress & Atahualpa 53 queries. 0,220 seconds. |
|||||
