Основатель школы Федор Борисович Смирнов
Условие задачи
Круглый торт весом в 1 кг разрезан на части прямолинейными разрезами. Известно, что два из этих разрезов проходят через центр торта, а третий не проходит. Докажите, что вес по крайней мере одной из получившихся частей составляет не менее 1/6 кг.
Эта задача предлагалась 8-классникам на заочной математической олимпиаде им. А.А. Леманского 19-27 октября 2012 года.
Решение задачи
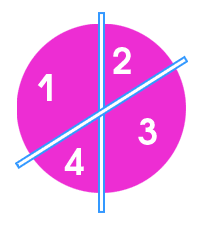
Два разреза, проходящие через центр, делят его на 4 куска, которые попарно равны.
Третий разрез не проходит через центр, поэтому он может пересекать либо один из первых двух разрезов, либо оба.
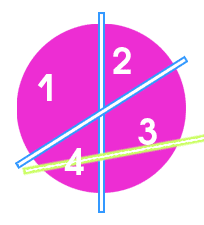
Случай 1. Третий разрез пересекает только один разрез. Тогда два куска (№1 и №2) остаются нетронутыми, а два других делятся каждый на две части.
Два нетронутых куска в сумме составляют 1/2, поэтому по крайней мере один из них не меньше 1/4 (легко доказывается методом от противного или по принципу Дирихле), и соответственно, не меньше 1/6.
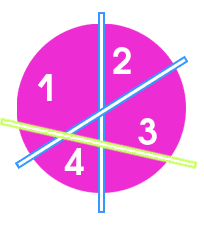
Случай 2. Третий разрез пересекает оба других разреза. Тогда только один из исходных кусков остается нетронутым (№2), а три остальных делятся каждый на две части.
Если нетронутый кусок больше либо равен 1/6, мы получаем нужный результат. Если же он меньше 1/6, то и равный ему кусок №4 меньше 1/6. И в сумме они составляют менее 2/6. Но тогда куски №1 и №3 (целиком, до того как третий разрез поделил их на части) в сумме составляют более 4/6.
После третьего разреза из кусков №1 и №3 получилось 4 новых кусочка, общей массой более 4/6. Но это означает, что хотя бы один из этих кусочков будет не менее 1/6 (доказывается методом от противного или по принципу Дирихле).
Вам была полезна эта страница? Покажите ее своим знакомым и друзьям!
Я буду признателен, если вы отправите ссылку знакомым — тем, кому может пригодиться информация о подготовке к поступлению в сильные школы и к участию в математических олимпиадах
— —
Приглашение в математический кружок в Новых Черемушках
Ваш ребенок учится в 4 классе? Вы планируете поступать в хорошую гимназию? Математический кружок в Новых Черемушках — хороший способ подготовить ребенка ко вступительным экзаменам, а также к участию в математических олимпиадах. Подробнее о кружке и о занятиях.
