Неделю назад дал ученикам своих мини-групп задание посчитать все треугольники, из которых состоят два рисунка:
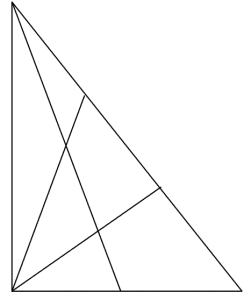 |
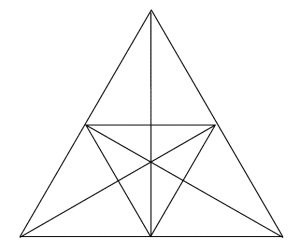 |
|
Легкий треугольник |
Сложный треугольник |
Задание 1.
К выполнению подобных заданий нужно подходить системно. (Именно этому я учу детей, которые собираются поступать в 5 класс математических гимназий и лицеев, на моем математическом кружке и в мини-группах в Новых Черемушках.)
Пронумеруем все элементы легкого треугольника.
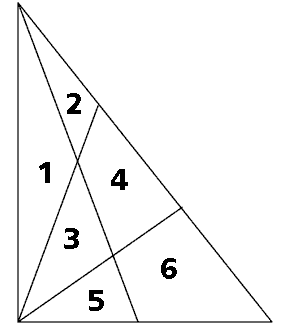 |
Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.
1. Из 1 элемента: 1, 2, 3, 5 — всего 4 треугольника (некоторые дети автоматически зачисляют в треугольники элементы № 4 и № 6 — это неправильно!).
2. Из 2 элементов: 12, 34, 56, 13, 35, 24 — всего 6 треугольников.
3. Из 3 элементов: 135, 246 — 2 треугольника.
4. Из 4 элементов: 1234 и 3456 — 2 треугольника.
5. Из 5 элементов — ничего нет.
6. Из 6 элементов — единственный 123456.
Итого: 15 треугольников.
Задание 2.
Сложное задание, требующее от детей внимательности, усидчивости и аккуратности в подсчетах. Пронумеруем все элементы легкого треугольника, причем цифр от 1 до 9 нам не хватит. Задействуем 10, 11 и 12.
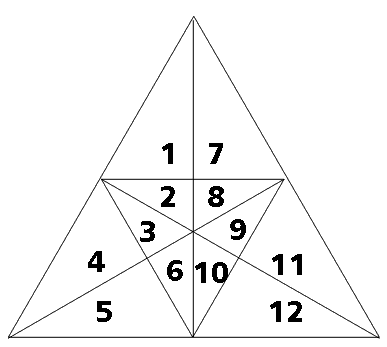 |
Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.
1. Из 1 элемента: все от 1 до 12 — это треугольники. Их 12 штук.
2. Из 2 элементов. Начинаем считать от вершины и движемся по часовой стрелке. 12, 17, 18, 9 11, 11 12, 12 10, 56, 54, 43. Не забудем про внутренние треугольники: 28, 9 10, 36. Насчитали снова 12 штук.
3. Из 3 элементов — отыщем их только во внутреннем треугольнике. 289, 36 10, 823, 9 10 6, 10 98, 632. Их 6 штук.
4. Из 4 элементов: 1234, 1236, 789 10, 789 11, 12 10 63, 12 10 65, 289 11, 4328, 56 10 9. Набрали еще 9 треугольников.
5. Из 5 элементов — ничего не нашел. Кто найдет — напишите, объявлю благодарность.
6. Из 6 элементов: 123456, 789 10 11 12, 12789 11, 12 10 6345, 56 10 9 11 12, 432178 — нарыли еще 6 штук. Плюс центральный: 236 10 98. Итого — 7 треугольников.
7. Ну и самый большой, из 12 элементов — 1 треугольник.
Кратко:
1 — 12
2 — 12
3 — 6
4 — 9
6 — 7
12 — 1
Итого: 47 треугольников. (Огромное спасибо мамам Антона и Маруси, которые помогли мне найти недостающие треугольники из 4-х элементов).
Бедные мои ученики…
Сочувствую. Но если им нужно сдавать вступительные экзамены в наши математические школы Юго-Запада (1533, 1534, 1543, 2007, Л2Ш, 1514 и т.д.) или участвовать в олимпиадах, то такая тренировка мозгов пойдет им только на пользу.
Так что их ждут новые задания. Что-то — полегче, что-то — потяжелее. Поступление в хорошую школу стоит того, чтобы усердно работать над заданиями, чуть-чуть выходящими за рамки школьной программы.
repetitorfb.ru/?p=1456

 Основатель школы Федор Борисович Смирнов
Основатель школы Федор Борисович Смирнов

