Основатель школы Федор Борисович Смирнов
Для решения используем метод подбора.
Вспомним, что если в олимпиадной задаче какие-то условия не даны, то они, возможно, и не нужны. То есть могут быть любыми, и ответ от этого не зависит.
Поскольку нам точно не сказано, как именно расположены квадраты, делаем вывод: размеры пересекающихся областей для разных конфигураций могут быть разными. Попробуем подобрать их.
Шаг 1. Площадь зеленого участка внутри маленького квадрата нам неизвестна, она может быть разной — в зависимости от расположения квадратов. Допустим, она равен 4.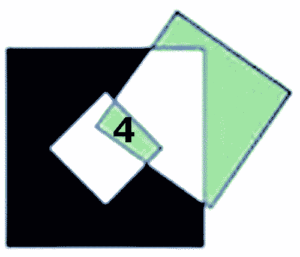
Шаг 2. Белая часть маленького квадрата (со стороной 3 см) теперь определяется однозначно:
3 · 3 — 4 = 5
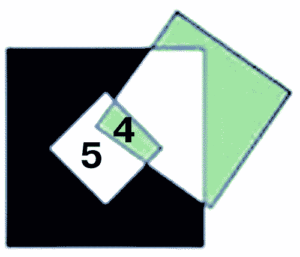
Шаг 3. Площадь зеленого участка в среднем квадрате снаружи большого квадрата так же не определена и зависит от расположения квадратов. Допустим, она равна 12.
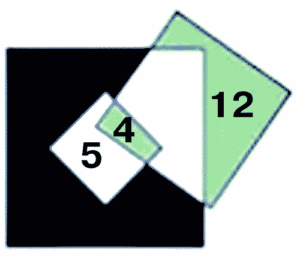
Шаг 4. Теперь однозначно вычисляется белый участок внутри среднего квадрата (со стороной 5 см):
5 · 5 — 12 — 4 = 9
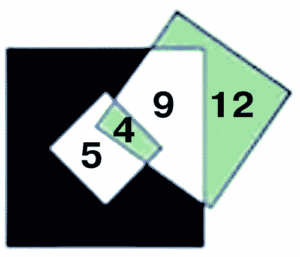
Шаг 5. Теперь вычислим площадь черного участка внутри большого квадрата (со стороной 7):
7 · 7 — (5 + 4 + 9) = 31
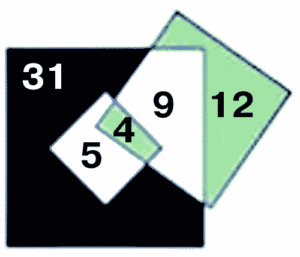
Шаг 6. Теперь мы можем ответить на вопрос задачи: на сколько черный участок больше зеленой области?
31 — (4 + 12) = 15.
Ответ: на 15.
Вы можете проделать такие же вычисления, задав другие значения на шаге 1 и 3. Ответ от этого не изменится.
