Основатель школы Федор Борисович Смирнов
Это задача №21 международного конкурса «Кенгуру» за 2006 год для 3-4 классов, которую я задавал на дом ученикам моего математического кружка в Новых Черемушках.
Условие задачи
Антон и Миша считают деревья, растущие вокруг пруда. Они двигаются в одном направлении, но начинают счет с разных деревьев. То дерево, которое Миша назвал двадцатым, для Антона оказалось четвертым, а дерево, которое Миша назвал десятым, для Антона оказалось сорок шестым. Сколько деревьев растет вокруг пруда?
Решение задачи
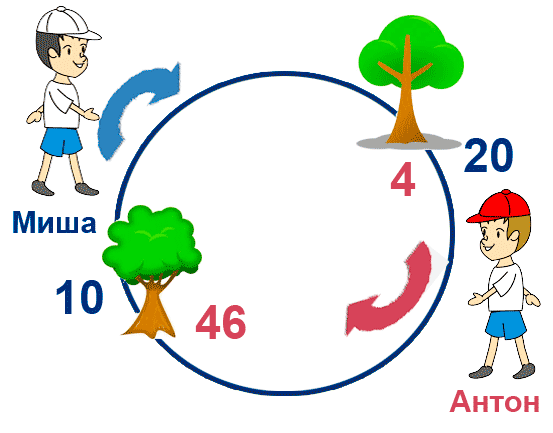
Нарисуем круг (пруд) и два дерева из задачи. Пусть нумерация Антона будет внутри круга, нумерация Миши — снаружи. Сначала дадим возможность Антону посчитать часть деревьев, а затем попросим Мишу посчитать оставшиеся.
Определим, сколько деревьев насчитал Антон от 4-го дерева до 46-го (включая и 4-ое, и 46-ое).
46 — 4 + 1 = 43 дерева.
(Напоминаю, что когда мы считаем, например, столбы от 5 до 10, то получаем не 10 — 5 = 5 столбов, а на 1 больше, т.е. 6)
Определим, сколько деревьев насчитал Миша.
20 — 10 + 1 = 11 деревьев.
Остается сложить 43 и 11 (получаем 54) и вычесть 2, поскольку оба граничных дерева посчитаны по два раза.
43 + 11 — 2 = 52 дерева.
Ответ: 52 дерева
Записывайтесь в мой математический кружок в Новых Черемушках
- Ваш ребенок учится в 3 классе?
- Вы через год планируете поступать в сильную гимназию (ЛИТ 1533, 1534, 1543, 1514, 2007 и другие)?
- Вы живете неподалеку от м. Новые Черемушки?
Записывайтесь в мой математический кружок или в мини-группу на следующий учебный год.
http://repetitorfb.ru/?p=1637
